Sólido de Johnson



En geometría, un sólido de Johnson es un poliedro estrictamente convexo, y cada una de sus caras es un polígono regular. Por otra parte, no es uno de los sólidos platónicos, ni uno de los sólidos arquimedianos, ni un prisma ni un antiprisma. No se requiere que todas las caras sean un mismo polígono, o que polígonos del mismo tipo se unan por los vértices. Un ejemplo de sólido de Johnson es la pirámide de base cuadrada con lados equiláteros J1, que presenta una cara cuadrada y cuatro triangulares.
En un sólido convexo estricto, al menos tres caras concurren a un vértice, y el total de sus ángulos es menor a 360°. Dado que un polígono regular tiene ángulos de al menos 60°, a lo sumo pueden concurrir cinco caras en cada vértice. La pirámide de base pentagonal (J2) es un ejemplo de grado 5 (máximo).
Aunque no existen restricciones respecto a que un determinado polígono forme una cara de un sólido de Johnson, los polígonos aplicables siempre tienen 3, 4, 5, 6, 8 o 10 lados.
Historia
[editar]En 1966 el matemático norteamericano Norman Johnson publicó una lista de 92 sólidos, dándoles nombre y número. Aunque no probó la imposibilidad de que existieran otros sólidos, hizo tal conjetura, y en 1969 Victor Zalgaller demostró que la lista era completa.
Entre los sólidos enumerados, la girobicúpula cuadrada elongada (J37) resulta única por tener vértices uniformes; cuatro caras concurren a cada vértice y su disposición es siempre la misma: tres cuadrados y un triángulo.
Nomenclatura
[editar]Los nombres listados son más descriptivos de lo que pueda parecer a simple vista. La mayoría de los sólidos de Johnson pueden construirse añadiendo una o más pirámides, cúpulas o rotondas en una de las caras de un prisma o antiprisma.
- Se denomina cúpula al poliedro que tiene dos polígonos regulares paralelos, unidos lateralmente por triángulos equiláteros y cuadrados alternándose unos y otros.
- La rotonda dispone también, como la cúpula, de dos polígonos regulares paralelos, pero se unen lateralmente por triángulos y pentágonos alternados.
Junto a estos tres poliedros se pueden utilizar para la construcción de los sólidos de Johnson; los sólidos platónicos, de Arquímedes, prismas y antiprismas.
El modo en que se combinan los distintos sólidos, se reflejan en su nombre mediante los siguientes términos y sufijos:
- Bi- significa que hay dos copias de un sólido dado unidas base con base. En el caso de las cúpulas y rotondas, se pueden unir de manera que se encuentren caras similares (orto-) o disimilares (giro-). Según esta nomenclatura, un octaedro sería una bipirámide cuadrada, un cuboctaedro sería una girobicúpula triangular y un icosidodecaedro sería una girobirrotonda pentagonal.
- Elongado significa que se ha unido un prisma a la base de un sólido dado o entre las bases que forman un sólido dado. Según esta nomenclatura, un rombicuboctaedro sería una ortobicúpula cuadrada elongada.
- Giroelongado significa que se ha unido un antiprisma a la base de un sólido dado o entre las bases que forman un sólido dado. Un icosaedro sería una bipirámide pentagonal giroelongada.
- Aumentado significa que se ha unido una pirámide o cúpula a una de las caras del sólido dado.
- Disminuido significa que se ha quitado una pirámide o cúpula de un sólido dado.
- Giroide significa que se ha rotado una cúpula del sólido de forma que encaje de forma distinta. Un ejemplo está en la diferencia entre las orto- y las girobicúpulas.
Las tres últimas operaciones — aumento, disminución y giro — se pueden realizar más de una vez en un sólido lo suficientemente grande. Si se ha realizado una de estas operaciones dos veces, se indica con el prefijo bi- (por ejemplo, un bigiroide es un sólido que tiene dos de sus cúpulas rotadas); y si se ha realizado tres veces se indica con el prefijo tri- (por ejemplo, un sólido tridisminuido es aquel al que se le han quitado tres de sus pirámides o cúpulas).
A veces los prefijos bi- y tri- dan lugar a ambigüedad. En el caso de que sea necesario distinguir entre un sólido al que se han alterado dos caras paralelas y uno al que se han alterado dos caras oblicuas, se indica la diferencia con los prefijos para- y meta-, respectivamente. Por ejemplo, un sólido parabiaumentado es aquel al que se han aumentado dos caras paralelas, mientras que a un sólido metabiaumentado se le han aumentado dos caras oblicuas.
Enumeración
[editar]| º | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jn | Nombre | Desarrollo | Imagen | Vértices | Aristas | Caras | Caras según número de lados | Simetría | Grupo | |||||
| F3 | F4 | F5 | F6 | F8 | F10 | |||||||||
| 1 | Pirámide cuadrada | 
|
5 | 8 | 5 | 4 | 1 | C4v | Prismatoides y rotondas | |||||
| 2 | Pirámide pentagonal | 
|
6 | 10 | 6 | 5 | 1 | C5v | ||||||
| 3 | Cúpula triangular | 
|

|
9 | 15 | 8 | 4 | 3 | 1 | C3v | ||||
| 4 | Cúpula cuadrada | 
|

|
12 | 20 | 10 | 4 | 5 | 1 | C4v | ||||
| 5 | Cúpula pentagonal | 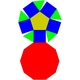
|

|
15 | 25 | 12 | 5 | 5 | 1 | 1 | C5v | |||
| 6 | Rotonda pentagonal | 
|

|
20 | 35 | 17 | 10 | 6 | 1 | C5v | ||||
| 7 | Pirámide triangular elongada (o tetraedro elongado) | 
|

|
7 | 12 | 7 | 4 | 3 | C3v | Pirámides modificadas y bipirámides | ||||
| 8 | Pirámide cuadrada elongada (o cubo aumentado) | 
|

|
9 | 16 | 9 | 4 | 5 | C4v | |||||
| 9 | Pirámide pentagonal elongada | 
|

|
11 | 20 | 11 | 5 | 5 | 1 | C5v | ||||
| 10 | Pirámide cuadrada giroelongada | 
|

|
9 | 20 | 13 | 12 | 1 | C4v | |||||
| 11 | Pirámide pentagonal giroelongada (o icosaedro disminuido) | 
|

|
11 | 25 | 16 | 15 | 1 | C5v | |||||
| 12 | Bipirámide triangular | 
|

|
5 | 9 | 6 | 6 | D3h | ||||||
| 13 | Bipirámide pentagonal | 
|

|
7 | 15 | 10 | 10 | D5h | ||||||
| 14 | Bipirámide triangular elongada | 
|

|
8 | 15 | 9 | 6 | 3 | D3h | |||||
| 15 | Bipirámide cuadrada elongada (o cubo biaumentado) |

|

|
10 | 20 | 12 | 8 | 4 | D4h | |||||
| 16 | Bipirámide pentagonal elongada | 
|

|
12 | 25 | 15 | 10 | 5 | D5h | |||||
| 17 | Bipirámide cuadrada giroelongada | 
|

|
10 | 24 | 16 | 16 | D4d | ||||||
| 18 | Cúpula triangular elongada | 
|

|
15 | 27 | 14 | 4 | 9 | 1 | C3v | Cúpulas y rotondas modificadas | |||
| 19 | Cúpula cuadrada elongada (Rombicuboctaedro disminuido) |

|

|
20 | 36 | 18 | 4 | 13 | 1 | C4v | ||||
| 20 | Cúpula pentagonal elongada | 
|

|
25 | 45 | 22 | 5 | 15 | 1 | 1 | C5v | |||
| 21 | Rotonda pentagonal elongada | 
|

|
30 | 55 | 27 | 10 | 10 | 6 | 1 | C5v | |||
| 22 | Cúpula triangular giroelongada | 
|

|
15 | 33 | 20 | 16 | 3 | 1 | C3v | ||||
| 23 | Cúpula cuadrada giroelongada | 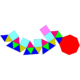
|

|
20 | 44 | 26 | 20 | 5 | 1 | C4v | ||||
| 24 | Cúpula pentagonal giroelongada | 
|

|
25 | 55 | 32 | 25 | 5 | 1 | 1 | C5v | |||
| 25 | Rotonda pentagonal giroelongada | 
|

|
30 | 65 | 37 | 30 | 6 | 1 | C5v | ||||
| 26 | Girobifastigium | 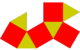
|

|
8 | 14 | 8 | 4 | 4 | D2d | |||||
| 27 | Ortobicúpula triangular (Cuboctaedro girado) |

|

|
12 | 24 | 14 | 8 | 6 | D3h | |||||
| 28 | Ortobicúpula cuadrada | 
|

|
16 | 32 | 18 | 8 | 10 | D4h | |||||
| 29 | Girobicúpula cuadrada | 
|

|
16 | 32 | 18 | 8 | 10 | D4d | |||||
| 30 | Ortobicúpula pentagonal | 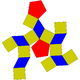
|
20 | 40 | 22 | 10 | 10 | 2 | D5h | |||||
| 31 | Girobicúpula pentagonal | 
|
20 | 40 | 22 | 10 | 10 | 2 | D5d | |||||
| 32 | Ortocupularrotonda pentagonal | 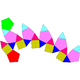
|

|
25 | 50 | 27 | 15 | 5 | 7 | C5v | ||||
| 33 | Girocupularrotonda pentagonal | 
|

|
25 | 50 | 27 | 15 | 5 | 7 | C5v | ||||
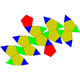
| 34 | Ortobirrotonda pentagonal (Icosidodecaedro girado) |
|

|
30 | 60 | 32 | 20 | 12 | D5h | |||||
| 35 | Ortobicúpula triangular elongada | 
|

|
18 | 36 | 20 | 8 | 12 | D3h | |||||
| 36 | Girobicúpula triangular elongada | 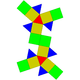
|

|
18 | 36 | 20 | 8 | 12 | D3d | |||||
| 37 | Girobicúpula cuadrada elongada (Rombicuboctaedro girado) |

|

|
24 | 48 | 26 | 8 | 18 | D4d | |||||
| 38 | Ortobicúpula pentagonal elongada | 
|

|
30 | 60 | 32 | 10 | 20 | 2 | D5h | ||||
| 39 | Girobicúpula pentagonal elongada | 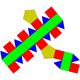
|

|
30 | 60 | 32 | 10 | 20 | 2 | D5d | ||||
| 40 | Ortocupularrotonda pentagonal elongada | 
|

|
35 | 70 | 37 | 15 | 15 | 7 | C5v | ||||
| 41 | Girocupularrotonda pentagonal elongada | 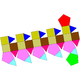
|

|
35 | 70 | 37 | 15 | 15 | 7 | C5v | ||||
| 42 | Ortobirrotonda pentagonal elongada | 
|

|
40 | 80 | 42 | 20 | 10 | 12 | D5h | ||||
| 43 | Girobirrotonda pentagonal elongada | 
|

|
40 | 80 | 42 | 20 | 10 | 12 | D5d | ||||
| 44 | Bicúpula triangular giroelongada (2 formas asimétricas) |

|

|
18 | 42 | 26 | 20 | 6 | D3 | |||||
| 45 | Bicúpula cuadrada giroelongada (2 formas asimétricas) |

|

|
24 | 56 | 34 | 24 | 10 | D4 | |||||
| 46 | Bicúpula pentagonal giroelongada (2 formas asimétricas) |

|

|
30 | 70 | 42 | 30 | 10 | 2 | D5 | ||||
| 47 | Cupularrotonda pentagonal giroelongada (2 formas asimétricas) |

|

|
35 | 80 | 47 | 35 | 5 | 7 | C5 | ||||
| 48 | Birrotonda pentagonal giroelongada (2 formas asimétricas) |

|

|
40 | 90 | 52 | 40 | 12 | D5 | |||||
| 49 | Prisma triangular aumentado | 
|

|
7 | 13 | 8 | 6 | 2 | C2v | Prismas aumentados | ||||
| 50 | Prisma triangular biaumentado | 
|

|
8 | 17 | 11 | 10 | 1 | C2v | |||||
| 51 | Prisma triangular triaumentado | 
|

|
9 | 21 | 14 | 14 | D3h | ||||||
| 52 | Prisma pentagonal aumentado | 
|

|
11 | 19 | 10 | 4 | 4 | 2 | C2v | ||||
| 53 | Prisma pentagonal biaumentado | 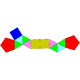
|

|
12 | 23 | 13 | 8 | 3 | 2 | C2v | ||||
| 54 | Prisma hexagonal aumentado | 
|

|
13 | 22 | 11 | 4 | 5 | 2 | C2v | ||||
| 55 | Prisma hexagonal parabiaumentado | 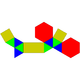
|

|
14 | 26 | 14 | 8 | 4 | 2 | D2h | ||||
| 56 | Prisma hexagonal metabiaumentado | 
|

|
14 | 26 | 14 | 8 | 4 | 2 | C2v | ||||
| 57 | Prisma hexagonal triaumentado | 
|

|
15 | 30 | 17 | 12 | 3 | 2 | D3h | ||||
| 58 | Dodecaedro aumentado | 
|

|
21 | 35 | 16 | 5 | 11 | C5v | Sólidos de Platón modificados | ||||
| 59 | Dodecaedro parabiaumentado | 
|

|
22 | 40 | 20 | 10 | 10 | D5d | |||||
| 60 | Dodecaedro metabiaumentado | 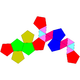
|

|
22 | 40 | 20 | 10 | 10 | C2v | |||||
| 61 | Dodecaedro triaumentado | 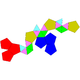
|

|
23 | 45 | 24 | 15 | 9 | C3v | |||||
| 62 | Icosaedro metabidisminuido | 
|

|
10 | 20 | 12 | 10 | 2 | C2v | |||||
| 63 | Icosaedro tridisminuido | 
|

|
9 | 15 | 8 | 5 | 3 | C3v | |||||
| 64 | Icosaedro tridisminuido aumentado | 
|

|
10 | 18 | 10 | 7 | 3 | C3v | |||||
| 65 | Tetraedro truncado aumentado | 
|

|
15 | 27 | 14 | 8 | 3 | 3 | C3v | Sólidos de Arquímedes modificados | |||
| 66 | Cubo truncado aumentado | 
|

|
28 | 48 | 22 | 12 | 5 | 5 | C4v | ||||
| 67 | Cubo truncado biaumentado | 
|

|
32 | 60 | 30 | 16 | 10 | 4 | D4h | ||||
| 68 | Dodecaedro truncado aumentado | 
|

|
65 | 105 | 42 | 25 | 5 | 1 | 11 | C5v | |||
| 69 | Dodecaedro truncado parabiaumentado | 
|

|
70 | 120 | 52 | 30 | 10 | 2 | 10 | D5d | |||
| 70 | Dodecaedro truncado metabiaumentado | 
|

|
70 | 120 | 52 | 30 | 10 | 2 | 10 | C2v | |||
| 71 | Dodecaedro truncado triaumentado | 
|

|
75 | 135 | 62 | 35 | 15 | 3 | 9 | C3v | |||
| 72 | Rombicosidodecaedro giroide | 
|

|
60 | 120 | 62 | 20 | 30 | 12 | C5v | ||||
| 73 | Rombicosidodecaedro parabigiroide | 
|

|
60 | 120 | 62 | 20 | 30 | 12 | D5d | ||||
| 74 | Rombicosidodecaedro metabigiroide | 
|

|
60 | 120 | 62 | 20 | 30 | 12 | C2v | ||||
| 75 | Rombicosidodecaedro trigiroide | 
|

|
60 | 120 | 62 | 20 | 30 | 12 | C3v | ||||
| 76 | Rombicosidodecaedro disminuido | 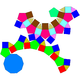
|

|
55 | 105 | 52 | 15 | 25 | 11 | 1 | C5v | |||
| 77 | Rombicosidodecaedro paragiroide disminuido | 
|

|
55 | 105 | 52 | 15 | 25 | 11 | 1 | C5v | |||
| 78 | Rombicosidodecaedro metagiroide disminuido | 
|

|
55 | 105 | 52 | 15 | 25 | 11 | 1 | Cs | |||
| 79 | Rombicosidodecaedro bigiroide disminuido | 
|

|
55 | 105 | 52 | 15 | 25 | 11 | 1 | Cs | |||
| 80 | Rombicosidodecaedro parabidisminuido | 
|

|
50 | 90 | 42 | 10 | 20 | 10 | 2 | D5d | |||
| 81 | Rombicosidodecaedro metabidisminuido | 
|

|
50 | 90 | 42 | 10 | 20 | 10 | 2 | C2v | |||
| 82 | Rombicosidodecaedro giroide bidisminuido | 
|

|
50 | 90 | 42 | 10 | 20 | 10 | 2 | Cs | |||
| 83 | Rombicosidodecaedro tridisminuido | 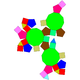
|

|
45 | 75 | 32 | 5 | 15 | 9 | 3 | C3v | |||
| 84 | Biesfenoide romo (Dodecaedro siamés) |

|

|
8 | 18 | 12 | 12 | D2d | Diversos | |||||
| 85 | Antiprisma cuadrado romo | 
|

|
16 | 40 | 26 | 24 | 2 | D4d | |||||
| 86 | Esfenocorona | 
|

|
10 | 22 | 14 | 12 | 2 | C2v | |||||
| 87 | Esfenocorona aumentada | 
|

|
11 | 26 | 17 | 16 | 1 | Cs | |||||
| 88 | Esfenomegacorona | 
|

|
12 | 28 | 18 | 16 | 2 | C2v | |||||
| 89 | Hebesfenomegacorona | 
|

|
14 | 33 | 21 | 18 | 3 | C2v | |||||
| 90 | Biesfenocíngulo | 
|

|
16 | 38 | 24 | 20 | 4 | D2d | |||||
| 91 | Bilunabirrotonda | 
|

|
14 | 26 | 13 | 7 | 3 | 5 | D2h | ||||
| 92 | Hebesfenorrotonda triangular | 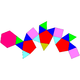
|

|
18 | 36 | 20 | 13 | 3 | 3 | 1 | C3v | |||
Sólido casi coincidente de Johnson
[editar]Un sólido casi coincidente de Johnson es un poliedro que se encuentra cerca de tener todas sus caras regulares, teniendo algunas caras levemente irregulares o todas sus caras irregulares con algún leve grado de distorsión, fallándole por poco a la definición de sólido de Johnson. Varios de estos poliedros son también simetroedros con algunas caras perfectamente regulares.
Véase también
[editar]Referencias
[editar]- Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pg. 169–200. Enumeración original de los 92 sólidos, y conjetura sobre que no existen otros.
- Victor A. Zalgaller (1969). Consultants Bureau, ed. Convex Polyhedra with Regular Faces. No ISBN. Primera prueba de que solo hay 92 sólidos de Johnson.
Enlaces externos
[editar] Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática. Portal:Geometría. Contenido relacionado con Geometría.
Portal:Geometría. Contenido relacionado con Geometría. Wikimedia Commons alberga una categoría multimedia sobre Sólidos de Johnson.
Wikimedia Commons alberga una categoría multimedia sobre Sólidos de Johnson.- Sylvain Gagnon, "Convex polyhedra with regular faces (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).", Structural Topology, No. 6, 1982, 83-95.
- Paper Models of Polyhedra Varios enlaces
- Johnson Solids por George W. Hart.
- Imágenes de los 92 sólidos categorizados
- Weisstein, Eric W. «Johnson Solid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Modelos VRML
- Juego para construir estos y otros sólidos Archivado el 26 de enero de 2021 en Wayback Machine. Bloques magnéticos
- Modelos VRML por Vladimir Bulatov
